1. 인지진단모형이란?
- 심리학에서 활용되는 심리측정 연구 모형으로 MacReady와 Dayton에 의해 1977년에 DINA라는 모델이 등장하게 되었고, Rupp & Templin에 의해 2008년에 Diagnostic Measurement: Theory, Methods, and Applications 라는 책이 출간되는 등 지속적으로 연구되고 있음. 실제로 국가수준의 많은 시험에서 이러한 인지진단모형을 적용하려는 시도가 계속되고 있음.
- 인지진단모형의 기본 개념은 피시험자의 평가 결과를 기반으로 세부적인 인지속성에 대한 숙달/미숙달을 판단하는 정보를 제공하기 위해 개별 피시험자인 학생이 시험에서 보인 문항반응(정답이라 생각해 선택한 보기)을 토대로 해당 피시험자이 각 인지요소 측면에서 어떠한 숙달 상태, 어느정도의 숙달 상태에 도달해 있는지 과학적으로 추론해주는 통계 모형입니다.
- 개별 피시험자의 인지상태를 통해 강/약점을 파악하고 강점 강화나 약점 보완을 위한 효과적인 피드백을 제공해주는 목적으로 사용됩니다. 인지진단모형을 통한 인지요소 숙달 여부 분석은 문항 난이도를 고려하여 인지요소 숙달 확률을 통계적으로 추정하는 방법입니다.
- 고전적인 CDM모델은 다양한 종류가 있습니다. Rule space Model, Fusion model, DINA(the deterministic inputs, noisy “and” gate)모형, DINO(the deterministic inputs, noisy “or” gate), Generalized diagnostic 모형 등이 있습니다. 이 고전적인 CDM 모델에 the hidden Markov model (HMM)이나 artificial neural network (ANN) 을 적용한 모델도 등장하고 있는 등 지속적인 응용이 이뤄지고 있습니다.
2. 인지진단모형의 요소
1) 인지요소 : 해당 시험의 각각의 개별 문항에 정답을 맞히는데 필요한 능력 (ability), 기능(skills), 지식(knowledge)이나 인지 과정(cognitive process) 등을 통합한 의미를 담고 있는 단어입니다.
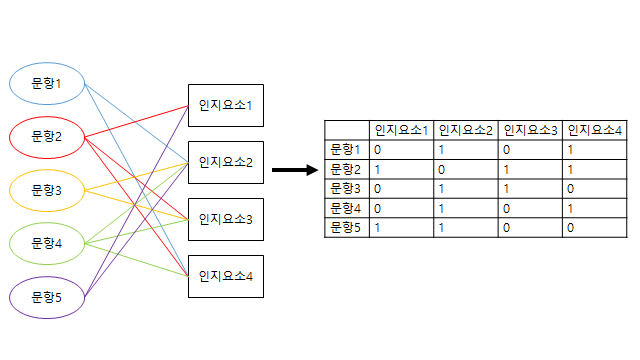
2) Q행렬 : 개별 문항과 이 문항에 필요한 인지요소들 간의 관계를 명시해 놓은 문항의 수*인지요소의 수 구조의 행렬을 말하는데 Q행렬의 각 원소는 인지요소를 습득하는 것이 문항을 푸는데 필요하면 1, 그렇지 않으면 0의 값을 가지는 one-hot encoding 방식을 사용하여 분류합니다.
예시) 5가지 문항과 4개의 인지요소에 대한 Q행렬
3. Q행렬 개발
Q행렬은 분야마다 다르기 때문에 다양한 방법으로 개발할 수 있지만, 인지진단의 목적으로 개발되지 않은 검사가 대부분이다. 하지만 이렇게 인지진단 목적으로 개발되지 않은 검사에 인지진단모형을 적용하고자 할 때 보통 4가지 단계를 사용한다고 한다.
일반적으로 인지진단모형을 사용하는 학업성취분야에서는 다음과 같은 과정을 거친다고 한다.
1. 해당 검사의 전문가가 해당 검사에서 측정하고 있는 인지요소들을 정의한다. 이 때 사용할 수 있는 방법은 다양한데, 문항 검토, 선행 연구 결과 검토 등과 같은 다양한 기법을 사용할 수 있다.
예) 수능국어의 경우에서 해당 문항이 화법-작문-문학-비문학 중 어떤 인지요소를 측정하고 있는지 정의
2. 1에서 정의된 인지요소와 개별 문항 간의 관계를 위의 그림에서 본 것 처럼 0-1 로 구분한 Q행렬로 개발한다.
예) 화법-작문-문학-비문학 Q행렬
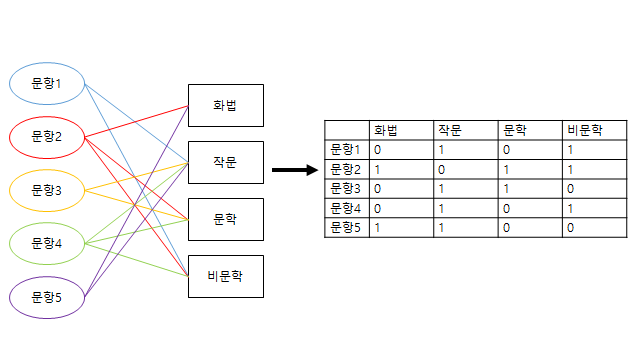
3. 학생(시험응시자-피시험자)별 실제 응답 자료를 바탕으로 Q행렬을 분석한다. 이 때 통계학적 인지진단모형을 사용하는데 DINA 등과 같은 모델을 적용한다.
4. 3의 분석 결과를 바탕으로 각 인지요소별로 숙달/미숙달의 정보를 학생(시험응시자-피시험자)들에게 평가 결과로 제공한다.
이렇게 분석한 결과가 정확하지 않다고 판단되면 Q행렬을 보완할 수 있다.
References
1. 김희경, 김부미. (2013). 인지진단모형을 활용한 수학 학업성취 결과 분석. 학교수학, 15(2), 289-314.
'데이터과학 > 데이터분석' 카테고리의 다른 글
| [Python] H2O 패키지를 활용하여 XGBoost 모델 구축하기 (0) | 2022.08.31 |
|---|---|
| [Windows10] RTX 3090, 3080 GPU tensorflow, pytorch 설치 (0) | 2020.12.21 |
| Github 깃허브 Windows10 설치 및 사용법 (2) | 2020.12.09 |

Comment