[풀잎스쿨 14기] semantic-segmenation-논문으로-입문하기 (U-Net_Elastic Deformations)

 

'본 포스팅은 모두의연구소(home.modulabs.co.kr) 풀잎스쿨에서 진행된 'semantic-segmenation' 과정 내용을 공유 및 정리한 자료입니다.'

1. introduction

Sementic Segmentation 분야에서 가장 유명하다 할 수 있는 논문인 Unet paper(https://arxiv.org/abs/1505.04597) 의 내용 중. 3.1 에서 Data Augmentation 에 관련하여 언급된 부분이 있었습니다. 

We generate smooth deformations using random displacement vectors on a coarse 3 by 3 grid . The displacements are sampled from a Gaussian distribution with 10 pixels standard deviation.

해당 부분인데, U-net이란 논문 자체가 Biomedical Image Segmentation 에 중점을 두고 나온 논문이기 때문에 이 내용을 이해하기 위해 추가적인 의학 논문에서 해당 Elastic Deformations 기술을 사용한 논문이면서 자세하게 설명하고 있는 논문을 찾아 이를 기반으로 여러 자료를 추가하며 정리하였습니다. 

 

Biomedical 분야에서 다양한 Deformations 방법 중 Elastic Deformations 을 사용한 이유는 다음과 같다.  
1) the small amount of available data

2) class imbalance 

이와 같은 문제를 해결하기 위해 elastic transformation을 도입하나, elastic transformation 이외에도 다른 augmentation도 충분히 사용 가능하다. 

 

>  Elastic Deformation 사용을 추천하는 경우 : 연속체에서 어떤 힘이나 시간 흐름으로 인해 변화가 발생하는 경우. 이 힘이 제거된 후 변형이 원래처럼 돌아오게 되면 이 변형을 탄성이라고 합니다. 이렇게 탄성이 있는 경우는 같은 물체라 해도 촬영 방법이나 각도 등에 의해서 다른 결과를 가져올 수 있으므로 이럴 때 사용하면 좋다고 하나 이 외의 경우에도 사용 (사람의 글씨체 차이에 따른 MNIST 적용 등에도 사용 했었음) 가능합니다. 

 

2. Method

1) 수평 및 수직 방향(x 및 y)에 대해 각각 임의의 stress (강도)가 generate 됨. 이 x,y 방향에 대한 강도를 다음과 같이 정의합니다. 

$$\Delta_{x}, \Delta_{y}$$

 

각 픽셀 및 방향에 대해 다음과 같은 범위 안에서 생성됩니다. 

$$\alpha \times [-0.5, 0.5] = [-0.5 \alpha, 0.5 \alpha]$$

이 범위 안에서 uniformly 하게 선택됩니다. 

 

아래의 가우스(가우시안) 필터(https://en.wikipedia.org/wiki/Gaussian_filter) 를 참조하시면 자세한 내용이 있습니다. 

$$G(\sigma)= g(x,y)= \frac{1}{2 \pi \sigma^{2}} \cdot e^{-\frac{x^{2} + y^{2}}{2\sigma^{2}}}$$

> x는 수평축 원점으로부터의 거리, y 는 수직축 원점으로부터의 거리, σ 는 가우스 분포의 표준 편차

 

2) 가까운 픽셀이 유사한 변위(displacement)를 갖도록하기 위해 결과 수평 및 수직 이미지에 Gaussian 필터를 별도로 적용합니다.

$$\Delta_{x} = G(\sigma) * (\alpha \times Rand(n,m))$$

$$\Delta_{y} = G(\sigma) * (\alpha \times Rand(n,m))$$

 

이러한 변환에는 두 가지 매개 변수가 있습니다.

1. 무작위 초기 변위에서의 최댓값 (alpha)
2. 가우시안 필터의 표준 편차에 의해 주어진 평활화 작업의 강도(sigma)

결과 패치 모양에 따라 이 값을 alpha = 300, sigma = 20 으로 설정. 그 후, stress 필드가 이미지, breast segmentation 마스크 및 Mass annotation 에 적용됩니다. 이것은 각 픽셀을 새로운 위치로 이동하고 정수 좌표에서 강도를 얻기 위해 spline interpolation 을 사용하여 수행됩니다.

$$I_{trans}(j + \Delta_{x}(j,k), k + \Delta_{y}(j,k)) = I(j,k)$$

위의 방정식에서 I와 Itrans는 각각 원본 이미지와 변환된 이미지입니다. 그리고 n * m 은 image dimensions입니다.

이러한 변형의 영향에 대한 예 그림은 아래와 같으며, 이는 유방암에 관련한 참조 연구 논문에서 발췌하였습니다. 

 

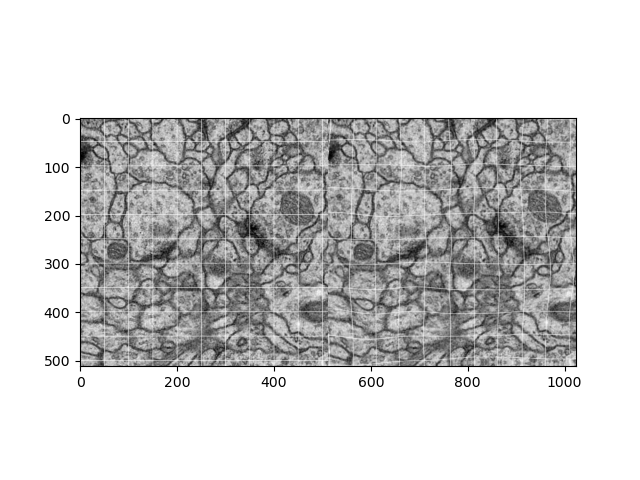
U-Net 예제에서 나온 Cell에 관련된 적용 이미지는 다음과 같습니다. 

512 * 512 왼쪽 원본 이미지 변형으로 U-Net 에서 사용한 Elastic Deformations 변형을 적용한 것이 오른쪽입니다. 

Elastic Deformations 에 대해 알아보았습니다!  이렇게 논문을 심층적으로 분석하고 함께 알아가는 풀잎스쿨 15기가 모집중이니 어서 풀잎스쿨 열차에 탑승해보세요! 

home.modulabs.co.kr/apply-flip15th/

 

 

References. 

Elastic Deformations for Data Augmentation in Breast Cancer Mass Detection, Eduardo Castro and Jaime S. Cardoso and J. C. Pereira, 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), 230-234p U-Net: Convolutional Networks for Biomedical Image Segmentation, Olaf Ronneberger and Philipp Fischer and Thomas Brox, 2015